Finding the shortest cheap mlb jerseys distance between two known points is generally straight forward:
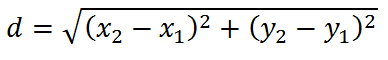
Where 1 and 2 are points, cheap nba jerseys x and y are their coordinates, an and d is the distance between them.
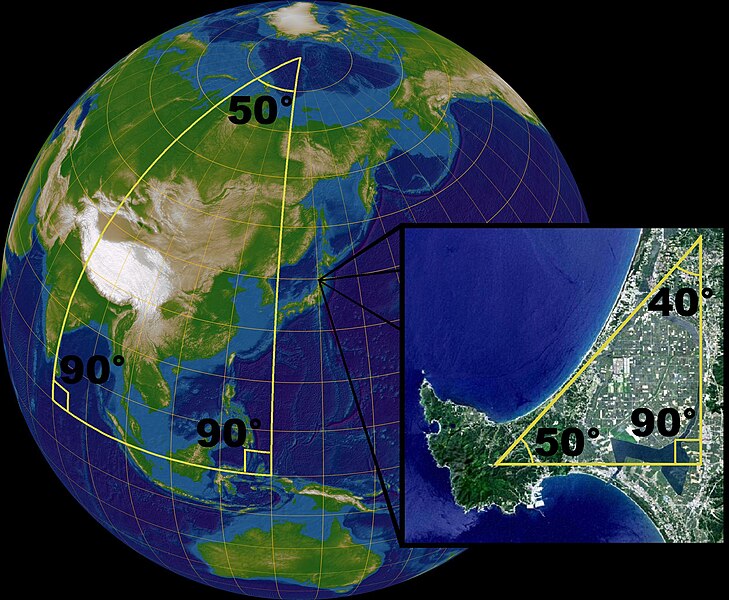
The problem of finding the distance between ??????? two points is Africa only generally straight forward because you’re probably used to working in Euclidean space. This type of geometry, however, makes an assumption that isn’t always true: that parallel lines never intersect. Seems obvious enough. But not all parallel lines are, well, parallel. Take, for example, the meridian lines of the Earth.
Those lines may look parallel on a map, but in reality… not so much.
Notice how the meridian lines converge and intersect at cheap nfl jerseys the poles. This can create some surprising results when you try to use your standard Euclidean math to solve problems on a spherical surface. For example, the assumption that the interior angles of a triangle add up to 180 degrees is no longer true. You may be able to get away using Euclidean geometry on a small-scale as a good vriendelijke approximation, but if you need better accuracy, or the scale is simply large, the fundamental formulas for solving problems like the distance between two points become useless.
Sorry Pythagoras. I’m sure you’re needed elsewhere.
Since the surface of a sphere is curved, finding the distance between two points along that surface will require some non-Euclidean geometry. A quick disclaimer: solving this type of problem when the Earth is your sphere is only an approximation since the Earth is only approximately spherical. If you’re working with spherical coordinates, you have everything you need to solve this problem. Well, once you know the haversine formula, that is:
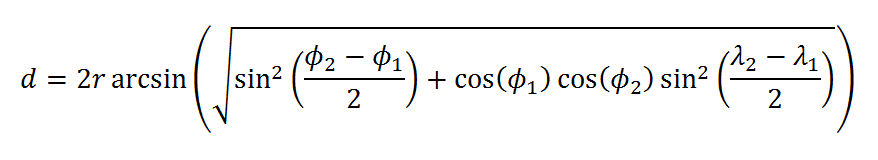
Where Φ represents latitude, λ longitude, r the radius of the sphere, and Path d the distance between the two points.
The haversine formula actually does use haversines, but this representation makes it a little easier to calculate with LabVIEW a standard calculator.
Congratulations, you are now a master of two out of three geometries. Go forth and know with a high degree of certainty that the distances you calculate are pretty darn accurate. Or wholesale mlb jerseys at least the math you use is.
Tags: gps, math, navigation
